ctr 综述

2022-09-29
作者 limhao
~11.60K 字

说些废话

点击率预估(CTR)在各种个性化在线服务中扮演着重要的角色，包括：计算广告、推荐系统和Web搜索等。

根据时间来分可以稍微看看这个图！

2007年以前都是 LR+人工特征工程为主

到了2010年以隐向量为代表的FM 模型，解决了人工组合特征的困扰

而在2014 年 facebook提出的 GBDT + LR 提出的一种树模型特点构建组合特征的思路

2015年以后，借助非线性自动组合特征能力的深度模型，开始成为业界的主流

从经典的DNN 到结合浅层的Wide&Deep 用于CTR预估模型的深度模型在这些年百花盛开。

各种交叉特征建模方法层出不穷，attention机制也帮助更好的适应业务，提升模型的解释性。

而核心问题离不开解决数据高维稀疏难题，自动化组合特征，模型可解释性等问题。

主要看了什么

深入 FFM 美团技术团队：深入FFM原理与实践

1. 前言 – CTR推荐是啥

ctr是啥

CTR指在搜索引擎中输入关键词后进行搜索，然后按竞价等因素把相关的网页按顺序进行排列出来，然后用户会选择自己感兴趣的网站点击进去；把一个网站所有搜索出来的次数作为总次数，把用户点击并进入网站的次数占总次数的比例叫点击率。

计算公式

计算公式为CTR=实际点击次数/展示量，即 Click / Show content。

CTR：点击通过率，Click-Through-Rate (点击通过比率)

ctr预估推荐

预测点击率(CTR）的算法被称为CTR预估算法，CTR预估的一系列算法经常用于推荐系统的排序阶段，其实有很多机器学习的方法或者深度学习的方法都可以作为CTR预估的算法，前提是这些算法的输出是一个0~1的概率值，并以概率作为分类的依据。

2. 问题定义以及评价

ctr推荐并不相同与ctr预估。其目标存在差距。

CTR预估起源于计算广告，因为关系到真金白银的定价问题，因此要求预估出来的CTR必须“绝对准确”。这是因为，假如给一个用户准备了A/B/C三个广告，那么无论预测CTR是0.9、0.8、0.6，还是0.5、0.4、0.3都不影响三个广告的展现顺序，但是向客户的收费却有天壤之别。

但是推荐系统只要求“相对准确”。假如ABC换成了三篇文章，只要能够将用户最喜欢的A排在第1位，次喜欢的B排在第2位，无论我们预测的CTR是0.9、0.8、0.6，还是0.5、0.4、0.3，用户都能接受。

2.1 定义

其输入是用户的点击和未点击的数据。通过分析，输出一个相对排序的item 进行推荐

2.2 数据集

数据集以点击数据集为主

同样的我看到的数据集类型基本都是广告这个类型

一定比的数据集有Criteo，azavu

其他的有 kdd12，ml-1m，iPinYou等

dataset	website	filed	records/k
Criteo	https://www.kaggle.com/c/criteo-display-ad-challenge/data	广告点击	45,850
azavu	https://www.kaggle.com/c/avazu-ctr-prediction/data	广告点击	40,428
iPinYou	http://contest.ipinyou.com/	广告点击	15,367
kdd2010	https://grouplens.org/datasets/mov	教育评分
ml-1m	https://grouplens.org/datasets/movielens/	电影评分	1000

2.3 常用评估指标

一定会比较的 AUC logloss

其他的 RelaImpr Rmse RIG

https://blog.csdn.net/fanfangyu/article/details/122885441

是一个模型的评价指标，只能适用于二分类模型的评价。

AUC（Area Under Curve）被定义为ROC曲线下与坐标轴围成的面积，

其中，ROC曲线全称为受试者工作特征曲线（receiver operating characteristic curve）

二元分类模型的预测结果有四个结局。即以下四种。

ROC曲线的横坐标是伪阳性率（也叫假正类率，False Positive Rate），纵坐标是真阳性率（真正类率，True Positive Rate），相应的还有真阴性率（真负类率，True Negative Rate）和伪阴性率（假负类率，False Negative Rate）。这四类指标的计算方法如下：

其中坐标轴的定义：

（1）伪阳性率（FPR）：判定为正例却不是真正例的概率，即真负例中判为正例的概率

（2）真阳性率（TPR）：判定为正例也是真正例的概率，即真正例中判为正例的概率（也即正例召回率）

（3）伪阴性率（FNR）：判定为负例却不是真负例的概率，即真正例中判为负例的概率。

（4）真阴性率（TNR）：判定为负例也是真负例的概率，即真负例中判为负例的概率。

关于曲线的绘制得看这个

https://blog.csdn.net/xiaohuihui1994/article/details/87987836

步骤大致分为三步：

按照属于“正样本”的概率将所有样本排序
将分类阈值设为最大，即把所有样例均预测为反例，所以得到此时的p和r均为0
依次将样本从高到低的样本score值作为阈值

logloss

二分类时 logloss 就是交叉熵

RelaImpr

$$
Relalmpr = (\frac {AUC(meadured\quad model)-0.5}{AUC(base\quad model)-0.5}-1)\times 100%
$$

RelaImpr代表相对于based model的相对改进指标，对于随机猜测的话，值AUC是0.5 （阿里DIN）

RMSE

均方根误差

$$
RMSE = \sqrt\frac{\sum_{i=1}^{N}(Predicted_i - Actual_i)^{2}}{N}
$$
均方根误差RMSE和标准差的计算公式也是高度近似的：标准差是用来衡量一组数自身的离散程度，而均方根误差是用来衡量观测值（真值）与预测值之间的偏差

相对信息增益(Relative Information Gain)

信息熵公式为：
$$
h(X) = - \sum_{i=1}^{n} p_i\log p_i
$$
在条件A一直的情况下，X的相对熵为：
$$
h(X|A) = \sum_{i=1}^{n} p_i(x_i|A)\log p_i(x_i|A)
$$
熵与条件熵的差值为信息增益：
$$
g(X,A) = H(X) - H(X|A)
$$
信息增益值的大小是相对数据集而言的，并没有绝对的意义，在分类问题比较困难的时候，也就是训练数据集的经验熵比较大的时候，信息增益的值比较大，反之，信息增益值会偏小。使用相对信息增益(信息增益比)可以对这一个问题进行校正，相对信息增益(Relative Information Gain):
$$
RIG =\frac {H(X) - H(X|A)}{H(X)}
$$
RIG指标不仅和模型的质量有关，还和数据集的分布情况有关；因此千万注意不可以使用RIG来对比不同数据集上生成的模型，但可以用来对比相同数据集上不同模型的质量差异。

2.4 模型大类

模型大类	提出时间	原理	优势	局限性
LR	2010年以前	使用线性权重组合每个单一的特征	具有效率高、易于快速部署、快速挖掘有效特征的优点	不具备特征交互的能力，交叉特征可能比单一特征具有更重要的影响
FM	2010	对Poly2中的权重矩阵W做矩阵分解，为每个特征学一个k为的向量表示。两个向量的内积表示特征对的重要性	FM可以捕获特征交互，同时可以在稀疏场景下有效的学习	FM忽略了这样一个事实: 当一个特性与来自其他域(Field)的特性交互时，它的行为可能会有所不同。
DNN	2015	利用深度网络，提高模型的交叉特征建模能力	偏重于挖掘高阶，增强了模型的表达能力	对低阶交叉特征信息利用不足，可解释性差
wide&deep	2016	通过联合训练的方式，同时获得线性模型（Wide）的记忆能力和深度模型（Deep）的泛化能力，提高模型的预测准确性和多样性	具有线性和深度两个特性	模型复杂训练时间长

3. 模型

3.1 LR模型

LR( Logistic Regression ) 是机器学习中一种线性分类模型，由于其简单、高效、易并行的特点，在实际生产环境中被广泛地应用。使用线性权重组合每一个单一特征

同样的在实际广告场景下的广告点击率预估问题。对于给定年龄、性别、教育程度、兴趣类目等用户侧特征，上下文特征，以及广告id，商品类型等广告侧特征。预测用户对于特征的点击概率。针对特征的做法是对各类特征进行one-hot编码，针对连续数值特征，会按照区间分段的方法将其离散化再进行one-hot编码。

对于LR的模型来说，需要提供成熟的特征工程工作，而对应的模型结构较为简单。对于其模型来说没有使用到组合特征，是一大问题。
$$
\hat{y}(x) = w_o + \sum_{i=1}^{n} w_ix_i
$$

poly2

模型有效的解决了LR的组合特征的问题，需要o（m2）的参数空间。特征xi和xj的两两组合用xixj表示，可见只有当xi和xj都为非零值时，组合特征（或称交叉项）在多项式模型中才有意义。在真实业务场景下，样本特征通常高维稀疏，而组合特征xixj的稀疏程度则更为严重。在这种极度稀疏的情形下，模型很难准确地学习出参数wij 。因为特征数据十分稀疏，模型在训练样本中从未见过有效的交叉项xixj，无法学习这个交叉项和label之间的关系。而参数无法准确学习，必然会严重影响模型效果。
$$
\hat{y}{Poly2}(x) = w_0 + \sum{i=1}^{n} w_ix_i +\sum_{i=1}^{n}\sum_{j=i+1}^{n}w_{ij}x_ix_j
$$

GBDT+LR

这个模型的主要思路是，先训练一个GBDT模型，然后利用训练好的GBDT对输入样本进行特征变换，最后把变换得到的特征向量作为LR模型的输入。

模型名	论文名	优势	缺陷	年份
LR		简单、高效、易并行的特点，在实际生产环境中被广泛地应用	缺少组合特征	2007
poly2		相较于LR 添加了组合特征	稀疏特征向量会变得更加稀疏，无法收敛。权重参数由n直接上升到 n2，增加了训练复杂度	2010
GBDT+LR	Practical Lessons from Predicting Clicks on Ads at Facebook, KDD 2014	自动化对输入样本进行特征变化，相比仅使用LR或Tree模型，loss降低了3%	1）树模型在节点分裂时需要遍历特征集，通常不适用于海量离散ID类特征场景 2）引入级联模型误差，无法做end-to-end学习	2014

3.2 FM模型

解决了POLY2模型的缺陷，FM诞生。最主要的区别就是使用隐向量对交叉特征的处理。对每一个对应的向量学习隐权重向量，在交叉特征是，使用两个特征隐向量的内积作为交叉特征的权重。

$$
\hat{y}{FM}(x) = w_0 + \sum{i=1}^{n} w_ix_i +\sum_{i=1}^{n}\sum_{j=i+1}^{n}<v_i,v_j>x_ix_j
$$

直观上看，模型的计算复杂度是O(kn^2)，但经过如下对交叉项的优化，复杂度可以降低到O(kn)。

经过化简，FM模型的最终表达式为
$$
\hat{y}{FM}(x) = w_0 + \sum{i=1}^{n} w_ix_i + \frac{1}{2}\sum_{f=1}^{k}[(\sum_{j=1}^{p}v_{j,f}x_j)^2-\sum_{j=1}^{p}v_{j,f}^2x_j^2]
$$

通过将特征划分为不同的领域，将不同特征域的差异信息显式引入到模型中，台湾大学阮毓钦（YuChin Juan）等人提出了域感知的改进版FM，称为FFM（Field-aware Factorization Machines）模型。 FFM是在FM的基础上引入了“场”的概念而形成的新模型。在FM中计算特征xi与其他特征交互影响时，使用的都是同一个隐向量Vi。而在FFM中会按照事先规则分为多个场（Field），特征xi属于特定的场f。每个特征被映射为多个隐向量vi1，….vif，每个隐向量对应一个场。当两个特征Xi，Xj组合时，用对方对应的场对应的隐向量做内积。

优势：FFM可以捕获特征交互，考虑Field信息

缺点：参数量过多，在实际生产系统中，FFM的参数是不能接受的。

假设隐向量的长度为k，特征fields数量为f，FFM的参数空间大小为fkn+n+1。由于二次项不能化简，FFM的训练和预测时间复杂度为O(kn^2)。带来了巨大的内存消耗，以及过拟合的风险。

BiFFM

FFM的二次项参数量是FM的fields数量倍，实际应用中面临内存消耗大的困境。为此，任职于新浪微博的张俊林博士提出了新的解决方案，称为双线性FFM模型[4]，模型方程如下
$$
\hat{y}{BiFFM}(x) = w_0 + \sum{i=1}^{n} w_ix_i +\sum_{i=1}^{n}\sum_{j=i+1}^{n}v_iWv_jx_j
$$

双线性FFM的二次项和FM类似，仍然是将所有特征映射到同一隐空间。但不同于直接对隐向量做点积，为了增强模型的表达能力，双线性FFM在FM基础上增加了k×k参数矩阵W。

所有特征共享一个矩阵w

参数量为k^2

一个Filed 一个矩阵wi

参数量为f*k^2

一个filed组合一个Wij

参数量为f^2*k^2

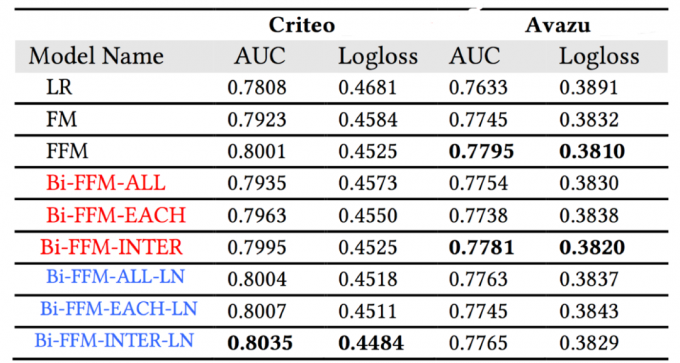
下表是双线性FFM在Criteo和Avazu两个公开数据集上的对比实验，结果表明，在内存消耗远小于FFM的情况下，双线性FFM效果接近于FFM，第三种类型的效果优于第一、第二种类型。一般情况下，在加入LayerNorm后，效果还有一定的提升。

FwFM（加权field型因子分解机）

通过FM,FFM的基础上做的工作，主要的思想：特征交互的重要性不同，因此要赋予不同的特征交互不同的权重。
$$
\hat{y}{FwFMs}(x) = w_0 + \sum{i=1}^{n} w_ix_i +\sum_{i=1}^{n}\sum_{j=i+1}^{n}x_ix_j<v_i,v_j>r_{F(i),F(j)}
$$

模型表达还是十分简洁，从复杂度分析，比FFM简介很多。相较于FM多了n*（n-1）/2的参数量

但是在效果上几乎接近于FFM，但在模型训练的难度上还是比FFM简单

FvFM（向量 Field 型因子分解机）

为了解决FwFM在特征交互权重上表达能力不够的问题。通过Field matrix的方式来计算特征交互重要性。

过程主要分成三步

FvFM是一个比FwFM自由度更加高，但是比FmFM自由度低的模型。此时的交互矩阵为每个维度有学一个权重

FmFM（矩阵 Field 型因子分解机）

把交互矩阵进行了扩展

3.3 DNN

如果说FM模型的更新，止步于filed层。在DNN这边就有了一个新的概念，embedding层。

embedding是用一个低维稠密的向量表示一个对象。方法起始于自然语言处理领域词向量生成问题的研究。

embedding技术对于深度学习推荐系统主要重要在于三个方面

推荐场景中大量使用one–hot编码对类别，id型特征进行编码，导致样本特征向量极其稀疏。几乎所有深度学习模型会使用embedding负责将高维稀疏特征向量转换成低维稠密向量
embedding本身就是极其重要的特征向量。相较于MF等传统方法产生的特征向量，embedding的表达能力更强，embedding几乎可以引入任何信息进行编码，使其本身包含大量有效信息
embedding对物品、用户相似度的计算是常用的推荐系统召回层技术。在局部敏感哈希等快速最近邻搜索等技术应用于推荐系统后，embedding更适用于对备选物品进行快速“初筛”，过滤出几百到几千量级的物品进行精排

主要解决embedding层收敛速度慢的问题。

FNN使用FM模型训练好的各特征隐向量初始化Embedding层的参数,相当于在初始化神经网络参数时引入了先验信息,这样一来神经网络训练的起点更接近于目标的最优点,加速了神经网络的收敛

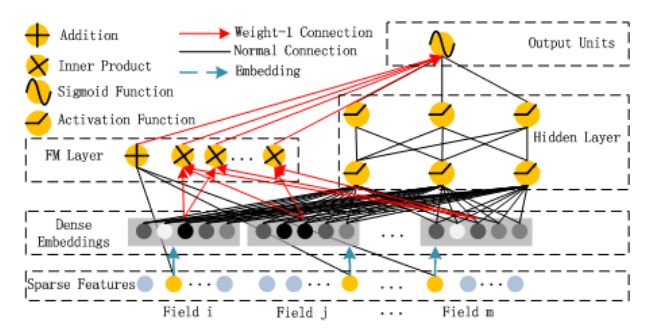
在结构上来看，FNN就是FM+MLP

优点

引入DNN对特征进行更高阶的组合，减少特征工程，在一定程度上增强了FM的学习能力

缺点

两阶段训练模式，在应用过程中不方便，且模型能力受限于FM表征能力的上限
FNN专注于高阶组合特征，但是却没有对低阶特征进行建模

PNN在embedding层和MLP全连接隐层之间增加了一个乘积层（product layer），用于更直接的建模两两特征的交互作用关系。乘积层包含z向量和p向量两部分，z向量由常数“1”向量和特征embedding相乘得到，因此z向量部分实际相当于特征embedding的直接拼接。p向量部分是PNN的核心，它是两两特征embedding进行“乘法”操作后的产物。

在使用不同乘法操作，将会带来不同的变体模型。IPNN( Inner Product-based Neural Network ),OPNN( Outer Product-based Neural Network )。从实验结果上看 PNN模型，包括IPNN、OPNN、PNN*（将inner product和outer product进行拼接），效果都要优于FNN。另外也能看到，基于深度神经网络的模型，效果普遍优于LR、FM线性模型，这说明非线性高阶特征建模有很重要的提升作用。

DeepCrossing

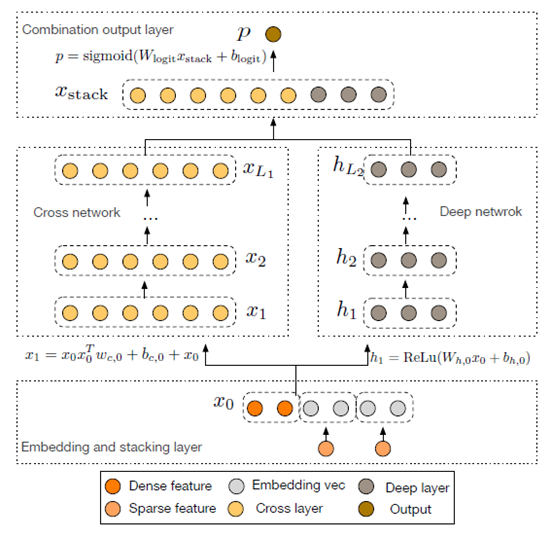
模型结构：

Stacking层负责将各特征embedding拼接成一个向量，随后使用级联的多个残差单元来代替传统MLP。引入残差单元是DeepCrossing的主要改进点，好处是可以使用更深的网络层数，建模更高阶的特征，增强模型的表达能力。

FNN、PNN和DeepCrossing模型都是在经典DND框架下演化而来的，它们都有效的提高了交叉特征的建模能力。但是对于低阶特征信息利用不足

3.4 wide&deep框架

对推荐系统的排序模型而言，定性地说，我们通常追求模型的记忆能力和泛化能力。一方面我们希望模型能准确记忆不同特征组合对预测目标的影响，以便依照已有的用户画像以及用户过去发生的行为使系统获得精准推荐能力，准确触达用户兴趣。另一方面，希望模型拥有一定的泛化能力，对未见过的或极少出现的特征组合，同样给出良好的预测结果，提高推荐内容的多样性。我们知道，线性模型以浅层形式直接学习稀疏组合特征权重，对训练数据中出现过的组合特征具有很好的记忆能力。而深度模型，稀疏特征被映射成低维稠密embedding向量，随后在深层全连接网络中获得充分交互，对具体的特征组合的“记忆”能力会减弱，但换来了更好的泛化效果。

基于这样的想法。 Google工程师在2016年提出了一种线性模型和深度模型的联合学习框架——Wide&Deep模型，期望通过联合训练的方式，同时获得线性模型（Wide）的记忆能力和深度模型（Deep）的泛化能力，提高模型的预测准确性和多样性。

wide端改进

DeepFM模型

Wide&Deep模型中Wide部分和Deep部分的特征输入是不同的，Wide部分的输入还需要依赖人工特征工程来挑选有效特征，为了减少特征工程依赖，华为工程师在2017年提出了DeepFM模型[12]。DeepFM仍然由Wide部分和Deep部分构成，不过Wide部分使用了FM来构建，利用FM自动学习二阶交叉特征的能力，代替需要人工交叉特征的LR。另外，Wide部分和Deep部分的底层输入特征以及特征embedding向量完全共享，能实现端到端学习。

Deep&Cross（DCN）模型

除了用FM代替LR以外，2017年发表的Deep&Cross Network（DCN）模型，提出了一种新的Cross网络来建模Wide部分，可以用更高效的方式实现更高阶的交叉。

deep端改进

NFM/AFM模型

对Deep部分的改进，Neural Factorization Machines（NFM）模型[14]是一个比较有效的方案，由Xiangnan He等人于2017年提出。NFM作者认为，经典DNN框架中的concat层只是把各特征embedding拼接成一个向量，并没有在底层利用好特征交互信息，只能依赖后面的MLP全连接层来建模特征之间的相互关系。但由于深度网络有梯度消失、梯度爆炸和过拟合等问题，DNN并不是很好优化，所以最终会导致模型效果有损失。所以NFM的主要改进点是，引入Bi-Interaction Pooling层，替代经典DNN的concat层，在底层增加足够的特征交互信息后，再馈入到MLP网络做进一步的高阶非线性建模。

引入新的子网络

xDeepFM

xDeepFM模型，全称eXtreme Deep Factorization Machine，是微软研究人员在Deep&Cross（DCN）模型基础上进行研究和改进后提出的。xDeepFM的主要创新点是，在传统Wide部分和Deep部分之外，提出了一种新的特征交叉子网络，Compressed Interaction Network（CIN），用于显式地以向量级vector-wise方式建模高阶交叉特征。

3.5 引入注意力机制

相比黑盒模型，注意力机制增强了可解释性，并且这些注意力权重是在翻译时根据输入动态计算的，模型的自适应能力也获得提升。基于这些优点，注意力机制在广告/推荐系统的排序模型上也有很多的探索和应用。

AFM模型可以认为是NFM模型的后续。在NFM模型中，不同域的特征embedding向量经过特征交叉池化层的交叉，将各交叉特征向量进行“加和”，输出最后由多层神经网络组成的输出层。

问题就在于 sum pooling操作，相当于将所有交叉特征赋予相同的权重，不考虑不同特征对于结果的影响程度，实际上消解了大量有用的信息。

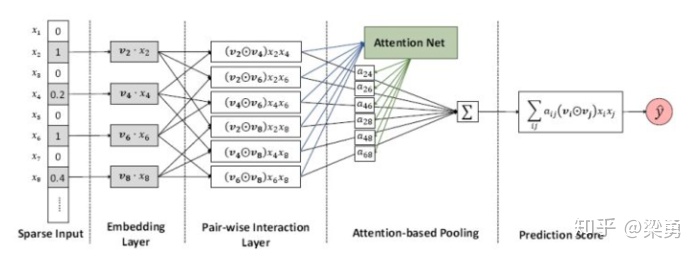
而模型通过引入注意力机制是通过在特征交叉层和最终的输出层之间加入注意力网络实现的。

图的前三部分都和FM是一样的。而后面的部分，则是AFM创新所在，就是attention net

AutoInt

2018年提出的AutoInt模型是一个使用多头自注意力机制增强模型解释性，同时又具备高阶交叉建模能力的模型

FiBiNET

FiBiNET，是结合特征重要性和双线性特征交互的CTR预估模型，由新浪微博机器学习团队发表在RecSys19。

其新颖的点是加入了senet layer 和 Bilinear-Interaction Layer

SENET

SENET Layer的主要作用是学习不同特征的重要度，对不同特征向量进行加权。即该Layer的输入为特征组embedding矩阵 E = [e1, e2, …, em]，Layer内部学习出每组特征的重要度 A = [a1, a2, …, am]，最后输出的“SENET-Like Embeddings”，V = A * E = [a1e1, a2e2, …, am*em]。SENET Layer本质上也是Attention机制

Bilinear-Interaction Layer：

原文作者认为传统的内积或哈达玛积形式难以有效对稀疏数据进行交叉特征建模，因此提出了一种双线性特征交叉方式（这种形式前文介绍双线性FFM时也有提到），

Deep Interest Network（DIN）[21]是阿里妈妈广告算法团队在2017年提出的，DIN是一个工业应用性很强的方案，特别是在电商领域。其中是为了解决传统DNN模型会将这些用户行为embedding向量通过固定的形式（sum/max/mean等）pooling成一个定长向量作为用户兴趣表示，所有用户的兴趣表示都被映射在一个相同的固定空间，而由于空间维度（即向量维度）的限制，用户兴趣的多样性特点无法得到充足的表达。

DIN对这个问题的解决方案是“局部激活”（Local Activation），即根据候选广告来自适应的为历史行为向量分配激活权重，以attention-based pooling的方式将其合并作为用户在该候选广告下的兴趣表示，使得与候选广告更相关的历史行为在用户兴趣表示中占更主导的作用。

核心模块Activation Unit

该论文的注意力模块是一大创新点，输入out product中候选物向量和用户历史行为向量进行交互（DIN模型b很清楚的解释了谁和谁交互），交互方式可以选择向量点乘、向量加或向量减（两个向量进行减法可以表示两者差异，结果小说明两个物品相似，加法相当于pooling，乘法表示两者之间相似度），文章中使用的是向量减，使得损失信息最少。交互是为了引入显性支持，利于后续建模，将交互后的向量与原始两个向量进行拼接，输入到多层感知机中，最后通过一个全连接层（可以看成与拼接向量同维度的一个向量进行点乘然后相加）得到这个拼接向量对应的权重，也就是这个用户历史行为向量的注意力得分。

DIEN

DIEN，全称Deep Interest Evolution Network[22]，也是来自阿里DIN的提出团队，是DIN的进化版，旨在挖掘用户行为背后的更高抽象语义的用户兴趣演化规律。DIEN的两个主要创新点：

兴趣抽取层（Interest Extractor Layer），利用GRU序列建模，从用户历史行为中抽取兴趣状态表示h(t)，并且引入辅助loss利用下一时刻的行为信息帮助指导当前时刻h(t)的学习，更准确的建模用户兴趣向量。
兴趣演化层（Interest Evolving Layer），引入AUGRU（GRU with attentional update gate）建模用户兴趣的演化过程，在AUGRU的隐状态更新中引入目标广告和兴趣向量的attention因子，目的是使最终输出给DNN网络的兴趣终态h’(T)和目标广告有更高的相关度。

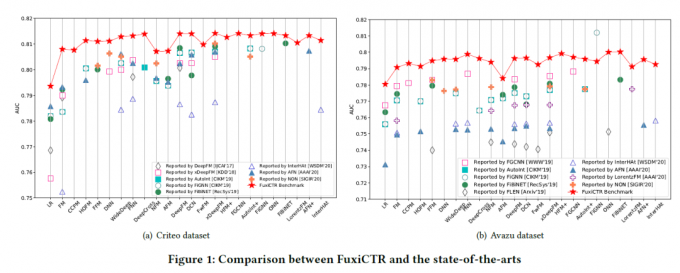
4. benchmark

BarsCTR: Open Benchmarking for Click-Through Rate Prediction

https://arxiv.org/abs/2009.05794

实验介绍

数据集

数据集	示例	特征总类	特征数	正比例
Criteo	46M	39	5.55M	26%
Avazu	40M	24	8.37M	17%

数据拆分

训练：验证：测试=8：1：1

评价指标

AUC 和 Logloss

实验结果

limhao博客

ctr 综述

说些废话

主要看了什么