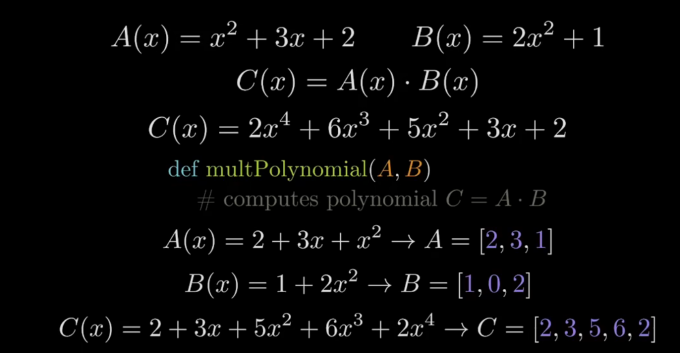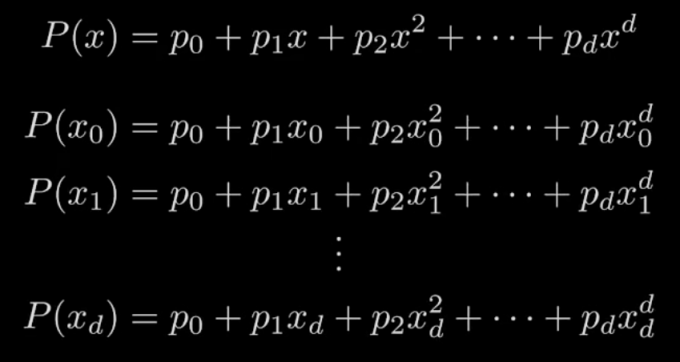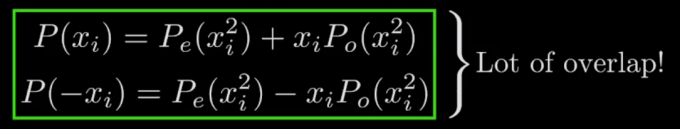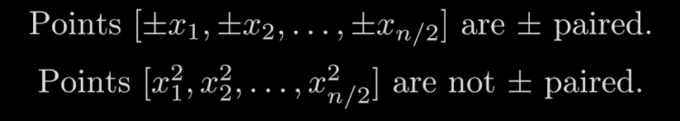6/3 日 经过两天的阅读
大致掌握了 快速傅里叶变换是个啥
在这里 致谢:
https://www.bilibili.com/video/BV1za411F76U
https://zhuanlan.zhihu.com/p/267276132
视频对于我理解不到的部分 知乎的文字部分做了充分的解释
0. 前言
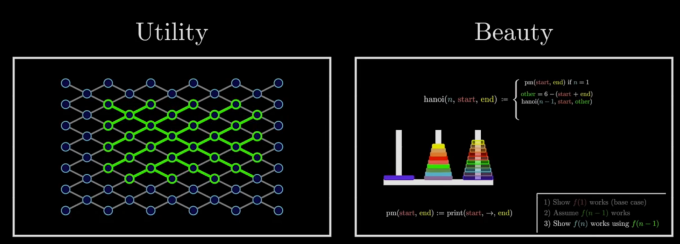
快速傅里叶是一个怎么样的算法
一个有效 且 漂亮的算法
1. 举个例子
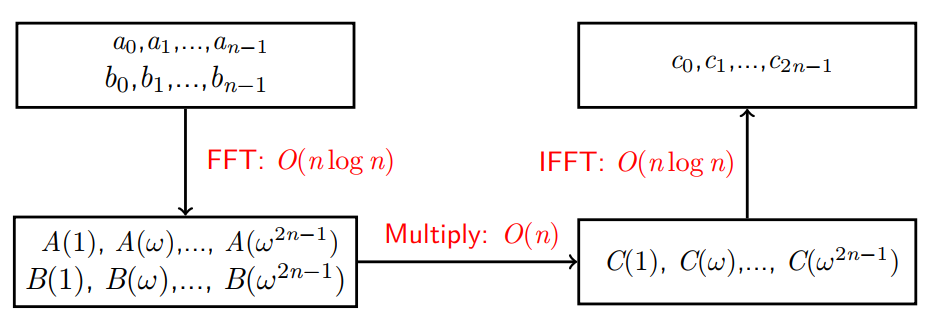
有一个多项式a 和一个多项式b
在a为两阶多项式 b同样为两阶多项式
算出来的c为四阶函数
对于一个d阶的多项式 可以通过 d+1 个点 来确认曲线
线性方程 转换成 矩阵形式
当点互不相同时,对于未知数而言,其系数矩阵为范德蒙矩阵,必可逆,故有唯一解,这唯一确定了多项式系数也即唯一确定了多项式
2. 回到方程本身
- 对于 方程进行多项式拆分成 偶函数和奇函数
- 然后划分成这个鬼样子
- 这个鬼样子的方程 有一个特性
为什么要去x^2 呢 应为 当x取正负的时候 x^2 总是为正
这样就能少算一个值 然后 多获得 一个点
后面有个奇函数项
其值是不存在配对项的 所以 这个循环是有问题的
3. 复数的提出
在这里 最创新的思维来了
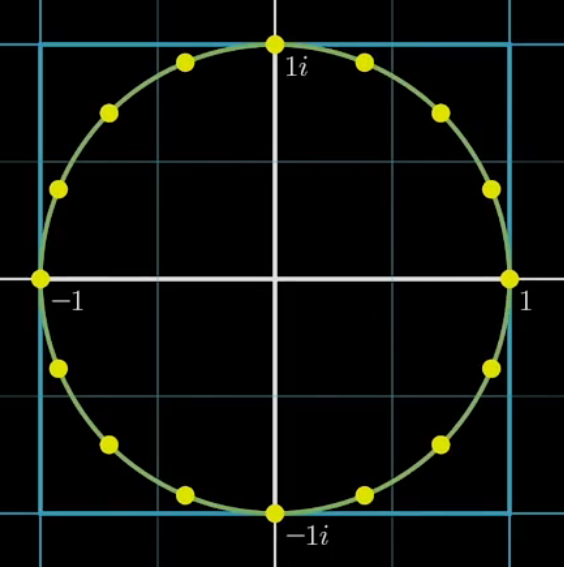
有一些复数的平方之后 依旧是正负成对出现
通过 将x替换成复数范围内的值 既可以完成我们点与点成对出现的目标
欧拉方程
使用w将多项式中x替换
其时间复杂度为
因为值是对应的 所以 只需要计算一半的值就好了