cin的沙雕理解

2022-04-16
作者 limhao
~1.58K 字

0. 前言

感谢：

https://www.jianshu.com/p/b4128bc79df0

https://zhuanlan.zhihu.com/p/371849616

https://zhuanlan.zhihu.com/p/57162373

https://zhuanlan.zhihu.com/p/193101514

在主流的FM与DNN的结合方法中，这个明显是并行的结构

大家晓得xdeepFM 这个东西嘛这个东西与deepFM 的区别是根本没有什么相似性

不信看看网络结构图

这个是deepFM

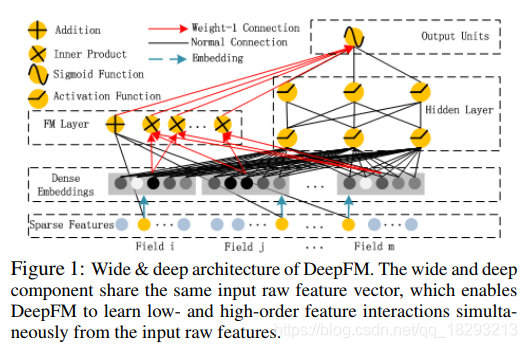
这个是大名鼎鼎的xdeepFM

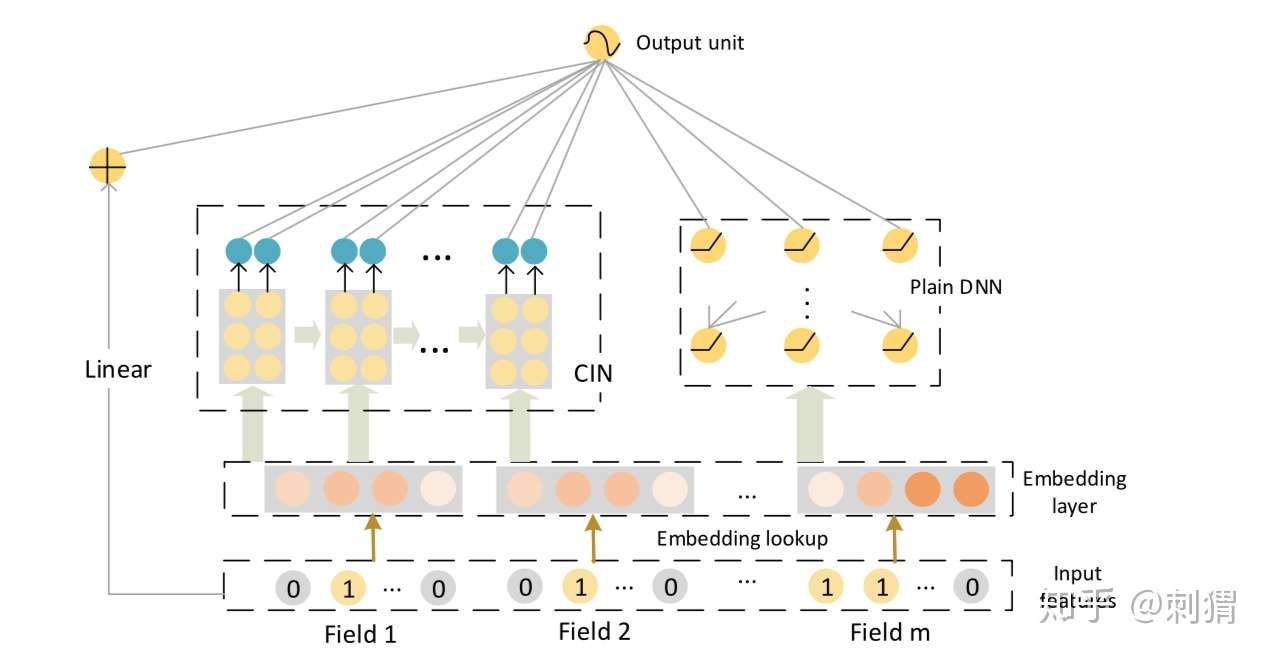
个人的瞎吉儿理解：在结构上，这两个玩意如果实在工程使用上我肯定会选择deepFM。xdeepFM在网络结构上就存在这一些复杂性，在deepFM的基础上增加了linear层和cin这个不晓得是啥的玩意。在理解中这个应该是我们xdeepFM 想要替换在deepFM 中 FM的部分

1. 模型的结构难点和自己的思考

既然说这个模型我都看了两天自然有其难点的地方 cin 的操作啊还有其为什么强的地方

1.1 难以理解的cin

讲明白一个东西首先先讲明输入输出

输入：field后的embedding层向量

输出：sum pooling后concat一个向量

1.2 介绍角色

说明啊

m 是 filed的个数

D 为 embedd维度

Hk 为第k层特征向量的数量

Xk 为第k层的隐向量

冤大头 $\mathbf{X}^0 \in \mathbb{R}^{m \times D}$

首先说明白冤大头的样子

embedd 1
embedd 2
********
embedd m

这个东西会反复使用（的确是冤大头）

假如说我有一个这样的隐藏层 $\mathbf{X}^k \in \mathbb{R}^{H_k \times D}$ 我这边感觉第一个隐藏层肯定是随机生成的

其与冤大头拥有一个相同长度的D边与隐藏层进行外积操作

于是可以得到一个长方形的过渡张量 $\mathbf{Z}^{k 1} \in \mathbb{R}^{H_k \times m \times D}$

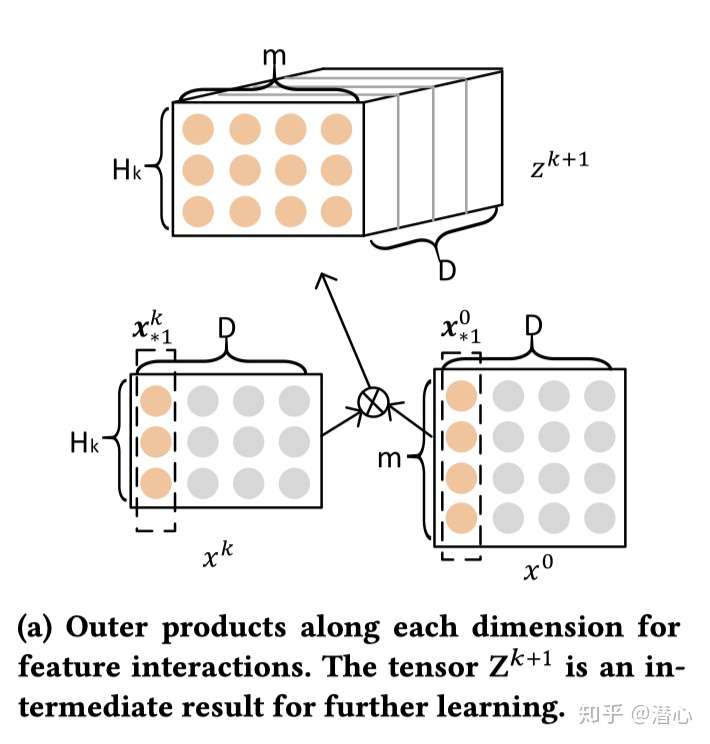
其作用是求出下一个隐藏层 $\mathbf{X}^{k 1} \in \mathbb{R}^{H_{k 1} \times D}$

1.3 下一个隐藏层求法

本人将用最简单的话来说明白下一个图的意思

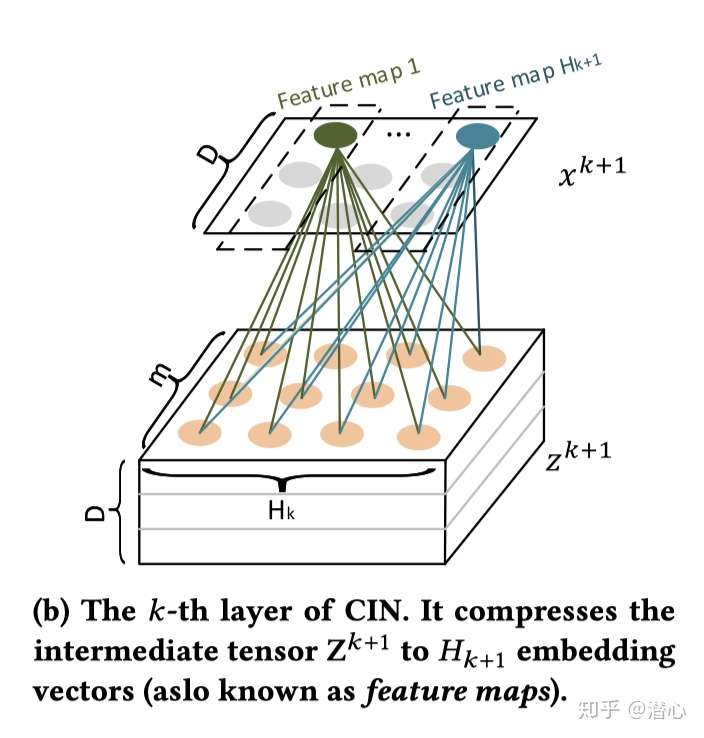
欧克图里面最直接就能看到一个躺着的张量，上面能看到，一个平铺的 $\mathbf{X}^{k 1} \in \mathbb{R}^{H_{k 1} \times D}$ 向量

其宽为D 长度为Hk+1

先从最基础的绿色的点开始

每一层都会得到一个绿色的点，张量的高为D 所以得到隐向量的宽为D
隐向量的长度为Hk+1,这个数据的设置没有任何根据属于随心所欲
绿色点的计算会使用到一整个面的橙色的点

1.4 张量的生成

我们获得了隐向量 $\mathbf{X}^{k 1} \in \mathbb{R}^{H_{k 1} \times D}$

将其与冤大头做外积既可以获得下一层的过渡张量

然后根据1.3的做法生成对应的隐藏层

1.5 （1.3，1.4）循环

噢噢噢噢终于有k个隐藏层了呢

1.6 汇总

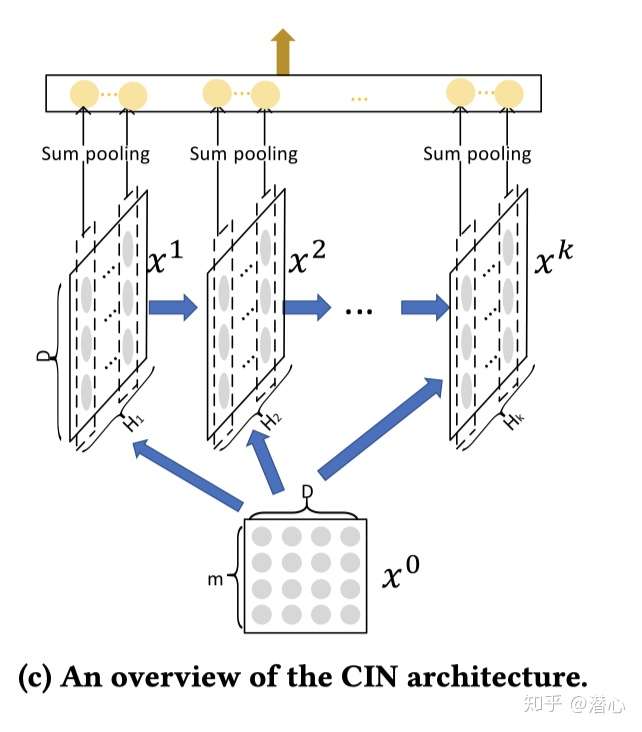
每个隐藏层为 $\mathbf{X}^k,k \in [1,T]$ ，对于第 $k$ 层，将所有的特征映射进行一个池化操作（sum pooling）【例如对上图Feature map 1向量进行一个累加】： $p_i^k=\sum_{j=1}^{D}\mathbf{X}^k_{i,j} \ \ \ i \in [1, H_k] \\$