感谢:
https://zhuanlan.zhihu.com/p/58160982
https://blog.csdn.net/bitcarmanlee/article/details/52143909
https://www.jianshu.com/p/152ae633fb00
-1 大前提
这个是无奈之举 发现 能写的太多了
强调一下 one-hot 编码问题
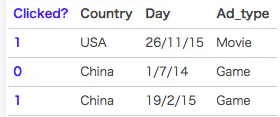
首先展示:
里面有 像click的分类值 有 country,day,ad_type则是对应的特征。对于这种categorical特征,一般都是进行one-hot编码处理。
在代码中是这样处理的
1 | (criteo_data.max(axis=0).astype(int) + 1).tolist()[:-1] |
画风一变!!
因为是categorical特征,所以经过one-hot编码以后,不可避免的样本的数据就变得很稀疏。举个非常简单的例子,假设淘宝或者京东上的item为100万,如果对item这个维度进行one-hot编码,光这一个维度数据的稀疏度就是百万分之一。由此可见,数据的稀疏性,是我们在实际应用场景中面临的一个非常常见的挑战与问题。
one-hot编码带来的另一个问题是特征空间变大。同样以上面淘宝上的item为例,将item进行one-hot编码以后,样本空间有一个categorical变为了百万维的数值特征,特征空间一下子暴增一百万。所以大厂动不动上亿维度,就是这么来的。
0. 前提
啊啊啊~~ 咱这一周2022年4月13日这个时间呐
发现!! FM 很重要 其理论的推理。现在看起来十分的重要
在工业界,这个模型 简直是yyds 其在CTR预估和推荐领域广泛使用
特征组合对于推荐排序是非常非常重要的,而FM这个思路已经很简洁优雅地体现了这个思想了(主要是二阶特征组合)
牛逼的点:
在embedding前夕 提出了类embedding的处理方式
- FM对于每个特征,学习一个大小为k的一维向量,于是,两个特征
和
的特征组合的权重值,通过特征对应的向量
和
的内积
来表示。这本质上是在对特征进行embedding化表征,和目前非常常见的各种实体embedding本质思想是一脉相承的,但是很明显在FM这么做的年代(2010年),还没有现在能看到的各种眼花缭乱的embedding的形式与概念。所以FM作为特征embedding,可以看作当前深度学习里各种embedding方法的老前辈。当然,FM这种模式有它的前辈模型吗?有,等会会谈。其实,和目前的各种深度DNN排序模型比,它仅仅是少了2层或者3层MLP隐层,用来直接对多阶特征非线性组合建模而已,其它方面基本相同。
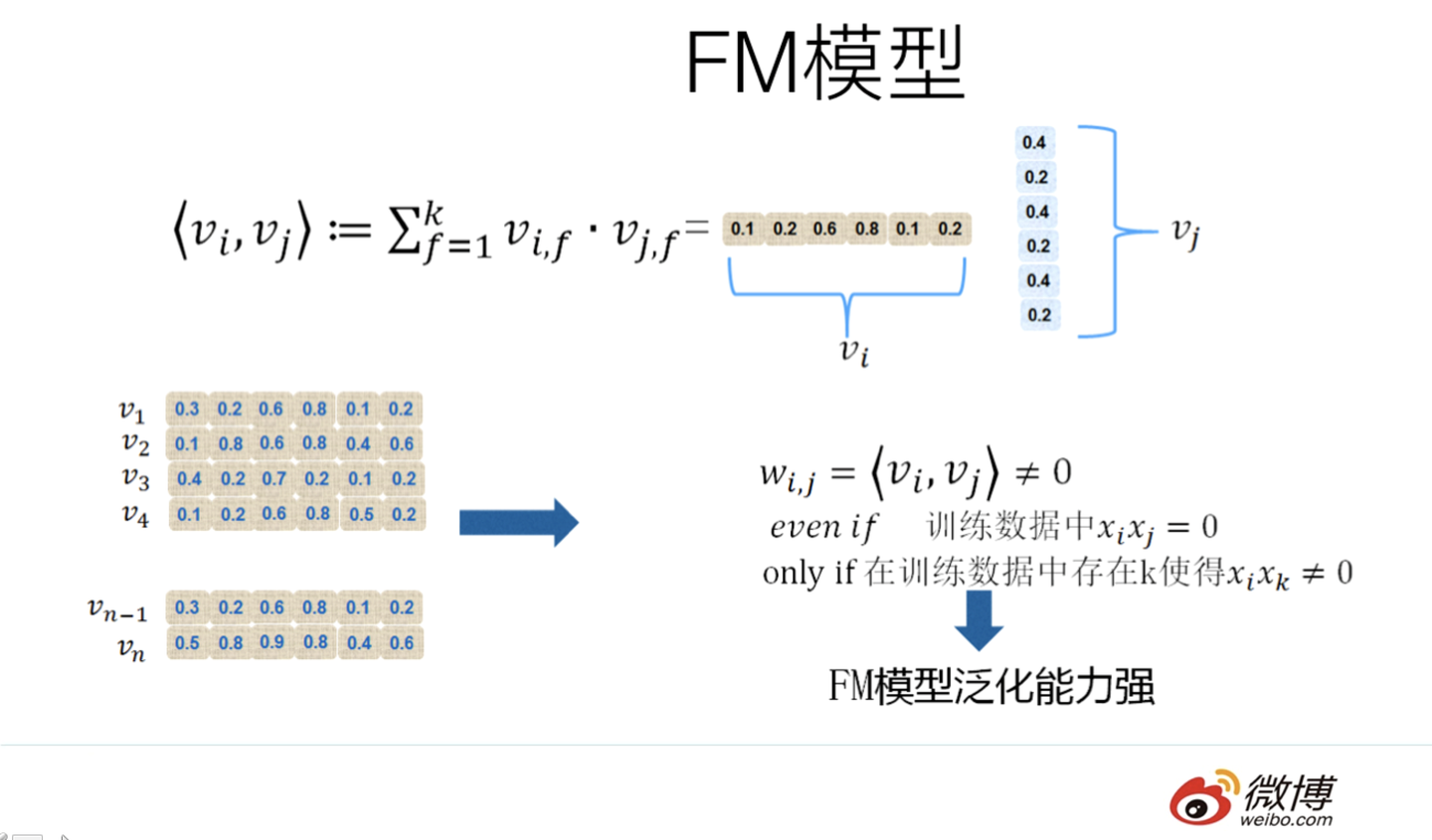
1. FM 前老弟(看起来就很复杂)
这个式子吧
从此公式可以看出组合特征一共有n(n-1)/2个,如果特征n上百个,组合特征上万个,就是任意两个wij相互独立,样本数据很稀疏,xixj为非零的项会非常的少,导致训练样本的不足,很容易导致参数 wij 不准确,最终将严重影响模型的性能和稳定性,在数据很稀疏的情况下,满足xi,xj都不为0的情况非常少,这样将导致ωij无法通过训练得出。
这个东西 在未来 将为一直成为推荐FM的垫脚石(敲砖引玉)
2. FM 老弟
在 工业界 还在使用
大多工业推荐排序系统采取LR这种“线性模型+人工特征组合引入非线性”的模式。因为LR模型具有简单方便易解释容易上规模等诸多好处,所以目前仍然有不少实际系统仍然采取这种模式。但是,LR模型最大的缺陷就是人工特征工程,耗时费力费人力资源,那么能否将特征组合的能力体现在模型层面呢?
使用了特征的隐向量 作为特征的相对应权重
上面的wij 使用 特征隐向量(辅助向量)的乘积
本人大白话讲一遍,啊啊啊 上面的式子太暴力,脑子思考一下就发现权重项太多,我在上面的这篇文献中发现这么一句:**对于任何正定实矩阵 只要k足够大,都存在k维向量组成的矩阵
使得
**
在这个公式下 这个V啊 就是辅助向量。
这个k相对于n来说 可太小了
所以 就从目前来说 权重系数 降低到了
3. 时间复杂度的减小
多图 警惕!
一个相对复炸的式子

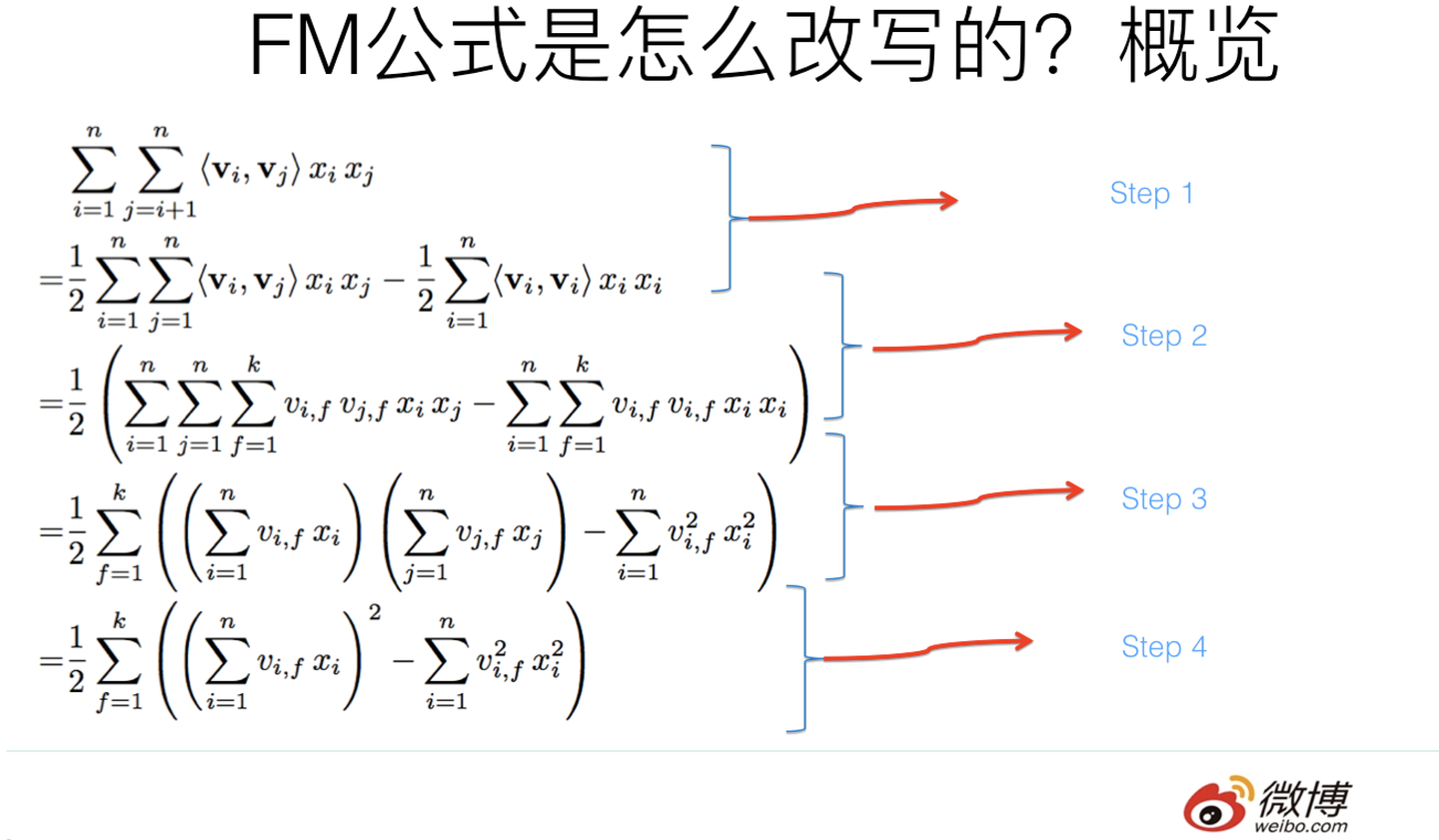
3.1 step1

3.2 step2
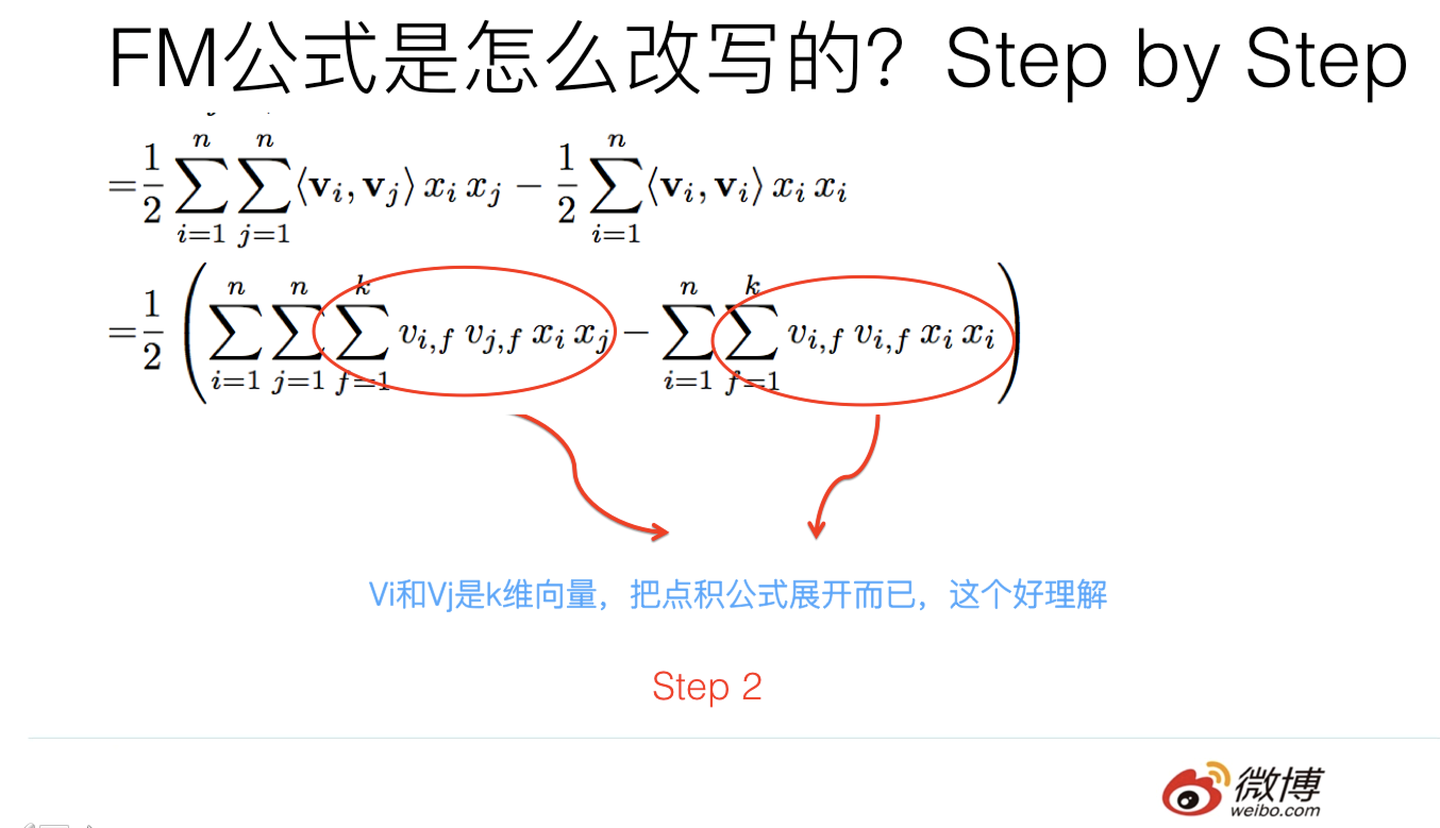
3.3 step3

第三步转换不是太直观,可能需要简单推导一下,很多人可能会卡在这一步,所以这里解释解释。
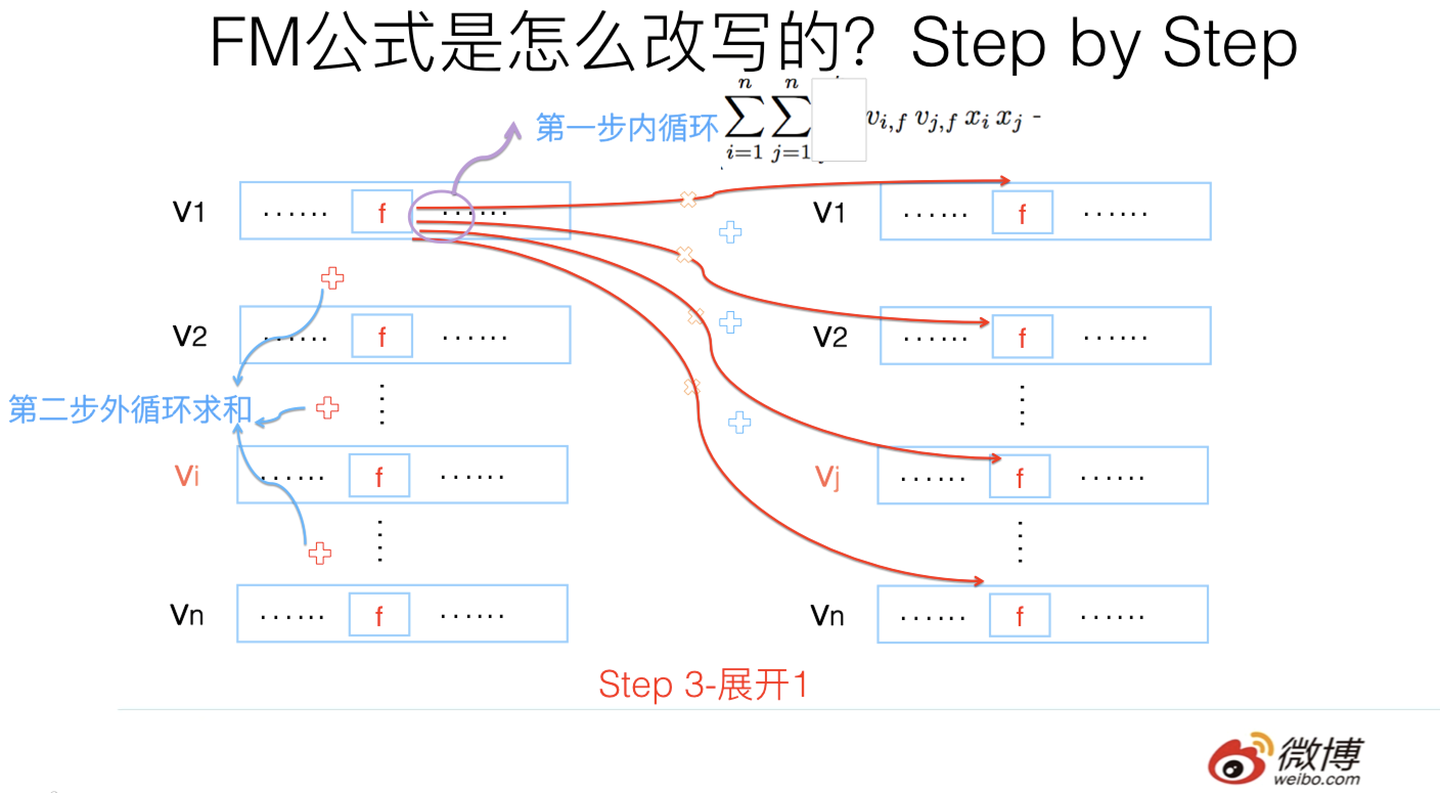
其实吧,如果把k维特征向量内积求和公式抽到最外边后,公式就转成了上图这个公式了(不考虑最外边k维求和过程的情况下)。它有两层循环,内循环其实就是指定某个特征的第f位(这个f是由最外层那个k指定的)后,和其它任意特征对应向量的第f位值相乘求和;而外循环则是遍历每个的第f位做循环求和。这样就完成了指定某个特征位f后的特征组合计算过程。最外层的k维循环则依此轮循第f位,于是就算完了步骤三的特征组合 
3.4 step4
对上一页公式图片展示过程用公式方式,再一次改写(参考上图),其实就是两次提取公共因子而已,这下应该明白了吧?要是还不明白,那您的诊断结果是数学公式帕金森晚期,跟我一个毛病,咱俩病友同病相怜,我也没辙了。