0. 说一些废话
这个文章 是大概阅读了 深度推荐系统 写出来的文章
很单纯 那时候 的文章
和热门印象很深的是 FM 和 MF 弄混了
1. 推荐系统技术架构
数据+模型
1.1 数据部分
通过特征工程,将客户端或服务端采集到的数据进行特征处理
1.2 模型部分
主题 一般由召回层,排序层,补充数据与算法层组成
2. 传统推荐模型(粗略整理)
2.1 协同过滤
分为 用户过滤和物品过滤
2.1.1 用户过滤(没人用)
公式一 余弦相似度
公式二 皮尔逊相关系数(减少了用户评分的影响)
2.1.2 物品过滤
基于历史数据,构建用户-物品共现矩阵(m*n)
计算共现矩阵两两向量间的相似性
获得用户历史行为数据的正反馈物品列表
利用物品相似度矩阵,针对目标用户历史行为中的正反馈物品,找出相似的topK物品
对于相似度进行排序,生成最终的推荐列表
2.2 矩阵分解算法–狗都不用
通过分解协同过滤生成的共现矩阵 得到用户和物品的隐向量
2.2.1 矩阵分解的求解方法
梯度下降 目标函数

2.3 特征交叉
单一特征的表达性 没有特征组合起来的表达性好 且 单一特征会损失一定量的信息
2.3.1 POLY2模型
暴力将特征n个 变成了$ n^2 $ 会将数据更加稀疏 增加训练复杂度
2.3.2 FM模型-隐向量特征交叉(嗯嗯嗯!)
感谢:https://zhuanlan.zhihu.com/p/109402085
个人的愚蠢回忆
说实话 有些东西一定要好好折磨一下 才能有新的收获 ! 比如这个
本人大白话讲一遍,啊啊啊 上面的式子太暴力,脑子思考一下就发现权重项太多,我在上面的这篇文献中发现这么一句:**对于任何正定实矩阵 只要k足够大,都存在k维向量组成的矩阵
使得
**
在这个公式下 这个V啊 就是辅助向量。
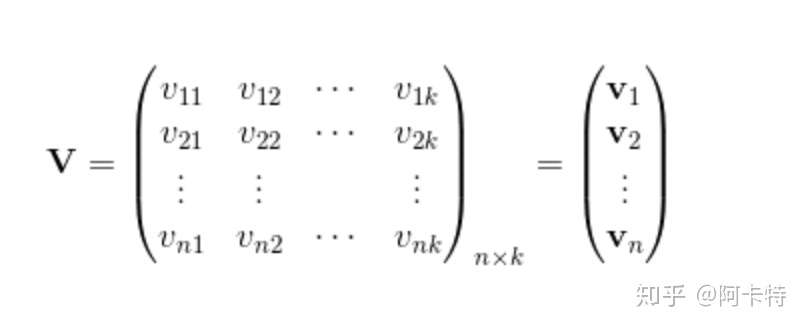
这个可爱的V呢 满足 (我想到了2077)
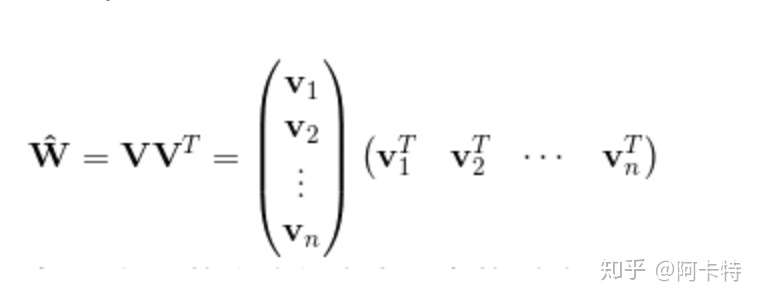
隐向量 就是为每个特征 学习一个隐权重向量(latent vector)
交互使用两个向量取内积就好
优势 1. 权重参数减少到nk
2. 训练复杂度降低到nk级别

2.3.3 FFM模型 特征域感知概念(可笑 咱把东西想简单了)
数据还是上一次的数据
FFM模型中引入了类别的概念,即field
在上面的广告点击案例中,“Day=26/11/15”、“Day=1/7/14”、“Day=19/2/15”这三个特征都是代表日期的,可以放到同一个field中。同理,Country也可以放到一个field中。简单来说,同一个categorical特征经过One-Hot编码生成的数值特征都可以放到同一个field,包括用户国籍,广告类型,日期等等
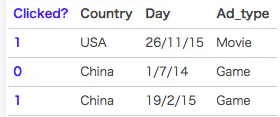
在FFM中,每一维特征 xi,针对其它特征的每一种field fj,都会学习一个隐向量 v_i,fj。因此,隐向量不仅与特征相关,也与field相关。也就是说,“Day=26/11/15”这个特征与“Country”特征和“Ad_type”特征进行关联的时候使用不同的隐向量,这与“Country”和“Ad_type”的内在差异相符,也是FFM中“field-aware”的由来
训练过程中,需要学习n个特征在f个域上的k维隐向量,参数 n * k * f 复杂度为 k$ n^2 $ 远多于FM模型的 nk个。此外,由于隐向量与field相关,FFM二次项并不能够化简,其预测复杂度是 O(kn^2)。
数据的处理
像Country,day 这样的categorical特征 可以通过 one-hot进行生成 如果是 像price这样的数值特征,则并不需要对其进行单独编码,但需要为其生成一个field。
个人的纯真理解(一眼顶真) 敲散说明白
假如说 我这里有4个field 一共有10个feature。
动动小脑就晓得 假如说 field1 对应 feat1到feat4
则对应 feat1到feat4 要生成对应的 field2到field4的权重(这个就是场感知啊!!!)
脑瓜子随便一想 哇靠 真复杂
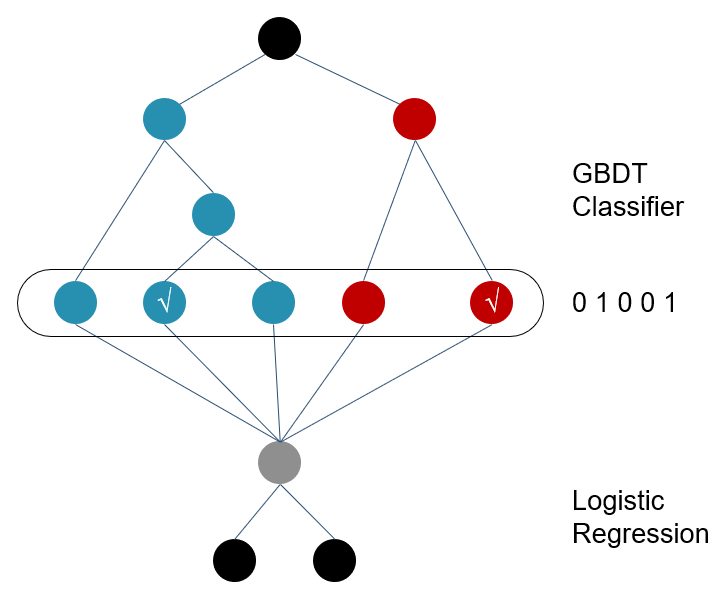
2.4 GBDT+LR 特征工程模型化
原始特征向量x,通过树分裂 将转化的特征类似于one-hot的向量来表示原始的特征,特征组合能力特别强
但是容易产生过拟合,以及这样的过程丢失了大量特征数值信息。
2.5 MLR 深度学习开始的曙光
2.5.1 MLR与LR的区别
普通的LR模型 无法拟合我们所需的曲线 但是MLR模型正常拟合出来了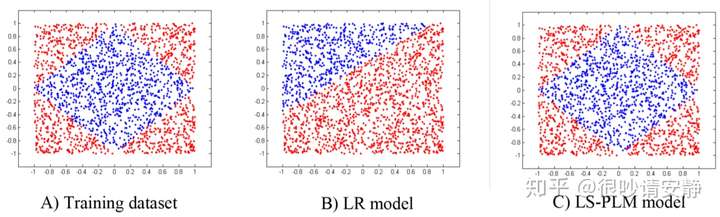
2.5.2 目标公式
如果m为1 则为普通的LR模型
当m越大 模型的拟合能力越强 而同样 需要的训练样本也变得更大 (阿里巴巴 经验12)
2.5.3 优点
- 端到端的非线性学习能力
- 模型稀疏性强